In our previous post, we discussed about training a perceptron using The Perceptron Training Rule. In this blog, we will learn about The Gradient Descent and The Delta Rule for training a perceptron and its implementation using python.

Why Gradient Descent ?

As we have discussed earlier, the perceptron training rule works for the training samples of data that are linearly separable. Another limitation is that if there are multiple local minima, then the previous rule might converge to a local minima instead of global minima. To overcome these limitations, we gonna use gradient descent for training our perceptron.

How it works ?

The idea behind the gradient descent or the delta rule is that we search the hypothesis space of all possible weight vectors to find the best fit for our training samples. Gradient descent acts like a base for BackPropogation algorithms, which we will discuss in upcoming posts.

Delta Rule can be understood by looking it as training an unthresholded perceptron which is trained using gradient descent . The linear combination of weights and the inputs associated with them acts as an input to activation function same as in the previous one.

O(x)= w.x

Before going into the activation function, we need to know how do we calculate the training error in the weights in case of misclassification. In Gradient Descent, we commonly use half the squared difference between the ouput and obtained value as the training error for our hypotheses.

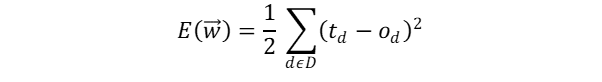
• D is set of training samples.
• t is the target ouput for training example ‘d’.
• o is the output of linear unit for training example ‘d’.

We would use the same unit step function as activation function for this example too.

Visualizing the Weight vectors and their Error values:

• w represents all possible weight vectors.
• J(w) represents the error values with respect to weight vectors.
• Parabolic path of error surface, which has a global minima at which the weight vectors are most suited for the training samples.

Derivation of Gradient Descent Rule

In Gradient Descent, we calculate the steepest descent along the error surface for finding local minima. For this we need to calculate the derivative of E with respect to the weight vector. This vector derivative is called Gradient of E with respect to weight vector w. The training rule can now be represented as :

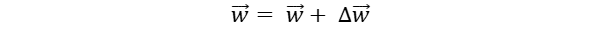
where E(w) is given by differentating the training errors of data samples with their correpsonding weight vectors. Substituting the whole thing in the above equation gives us:

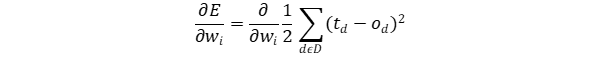
Differntiating the above equation (Fig 1.2)and substituing o = w.x in it would give us the result as follows:

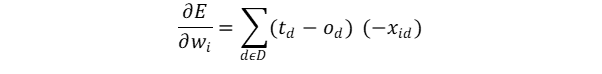
Therefore, by substituting Fig 1.3 in Fig 1.1 we get the final weight updation rule of Gradient Descent:

We have arrived at our final euqation on how to update our weights using delta rule. One more key difference is that, in perceptron rule we modify the weights after training all the samples, but in delta rule we update after every misclassification, making the chance of reaching global minima high.

Algorithm:

• Initialize the weight vector.
• For each training sample in dataset, apply the activation function and if any error occurs, update the weight according to the rule.
• Repeat it for finite number of epochs, to make it more accurate.

Implementation of Perceptron using Delta Rule in python

Wow, we entered our most interesting part. As perceptron is a binary classification neural network we would use our two-class iris data to train our percpetron. Our dataset contains 100 records with 5 features namely petal length, petal width, sepal length, sepal width and the class (species).

Create a python file namely Perceptron.py and class called Perceptron with a constructor which initializes weight vector to an empty list.

class Perceptron:
    def __init__(self):
        self.weights=[]

Define an activation function which takes each row in our dataset and does a dot product of it with weight vector and return 1 or 0 depending on the value of dot product.

#activation function
    def activation(self,data):
        activation_val=np.dot(self.weights,data)
        return 1 if activation_val>=0 else 0

Now we have our activation function and ready to checck for an misclassification. Now lets implements the fit method which incase of any misclassification updates the weight vector according to the delta rule. The fit method takes an input of training data and the associated class values along with the learning rate ( η ) and no.of epochs.

def fit(self,X,y,lrate,epochs):
        #initializing weight vector
        self.weights=[0.0 for i in range(len(X.columns)]
        #no.of iterations to train the neural network
        for epoch in range(epochs):
            print(str(epoch+1),"epoch has started...")
            for index in range(len(X)):
                x=X.iloc[index]
                predicted=self.activation(x)
                #check for misclassification
                if(y.iloc[index]==predicted):
                    pass
                else:
                    #calculate the error value
                    error=y.iloc[index]-predicted
                    #updation of associated self.weights acccording to Delta rule
                    for j in range(len(x)):
                        self.weights[j]=self.weights[j]+lrate*error*x[j]

Lets write a method predict which takes test values and predicts the outcome based on the weights of the neural network.

def predict(self,x_test):
        predicted=[]
        for i in range(len(x_test)):
            #prediction for test set using obtained weights
            predicted.append(self.activation(x_test.iloc[i]))
        return predicted

We are all set to drive our code for our iris dataset. Let’s take a second and implement accuracy method in our Perceptron class which returns accuracy depending on predicted values and original values.

def accuracy(self,predicted,original):
        correct=0
        lent=len(predicted)
        for i in range(lent):
            if(predicted[i]==original.iloc[i]):
                correct+=1
        return (correct/lent)*100

We always love to have a look on the updated weights in our neural network. Lets write a simple method get_weights which returns the weights of trained perceptron.

def getweights(self):
        return self.weights

Create another python file namely driver.py and import our iris.csv using pandas and split it into train and test data using train_test_split method from model_selection modeule of sklearn.

from Perceptron import Perceptron
import pandas as pd
from sklearn.model_selection import train_test_split
#read data from .csv file
data=pd.read_csv("iris.csv")
data.columns=["petal_length","petal_width","sepal_length","sepal_width","class"]
classes=data["class"]
data=data.drop(columns="class")
#splitting test and train data for iris
x_train,x_test,y_train,y_test=train_test_split(data,classes)
#training the percpetron
model=Perceptron()
model.fit(x_train,y_train,0.5,10)
pred=model.predict(x_test)
print("accuracy: ",model.accuracy(pred,y_test))
print("weights: ",model.getweights())

Yeah, we are all done. Lets run this driver.py code and have a look at our results😎😎.

Oh, we have got an accuracy of 100 percent on our test set. Feel free to train this perceptron on any other two-class data and check out the results. You can clone or download the whole source code and dataset in my github at https://github.com/TarunNanduri/Perceptron. Lets discuss about multilayer neural networks in our next blog. Until then cheers..🤞

Follow our blog on Facebook, to keep you updated on recent blog posts.